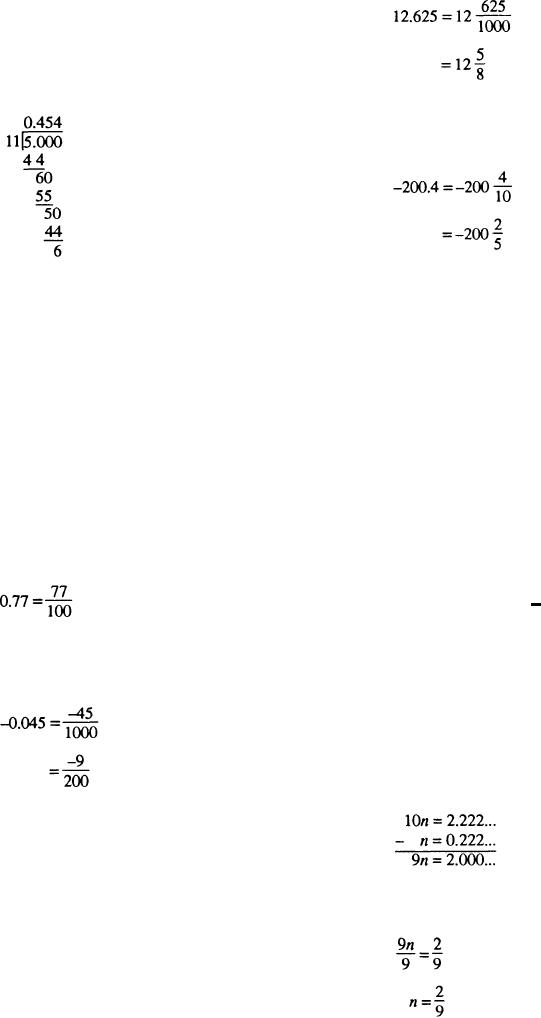
Example: Convert -72 5/11 to a decimal to the
nearest hundredth.
Solution: In this case, you would divide 5 by 11 to
one place past the desired place value of hundredths and
then round.
Example: Convert -200.4 to a fraction and reduce
to lowest terms.
Solution:
So, -72 5/11 = -72.45 to the nearest hundredth.
Converting Repeating Decimals
to Fractions
Converting Terminating Decimals
to Fractions
Converting a repeating decimal to a fraction is a
little more confusing than the conversions we have
To convert a terminating decimal to a fraction,
previously performed. A repeating decimal can be
count the number of digits to the right of the decimal
converted to a fraction by the following steps:
point. Move the decimal point that many places to the
1. Form an equation letting n equal the repeating
right, and write the answer you get over a denominator
decimal.
beginning with 1 followed by as many zeros as places
moved to the right. Reduce to lowest terms, if possible.
2. Multiply both sides of the equation by a multiple
of 10 in order to shift a set of the repeating
Example: Convert 0.77 to a fraction.
pattern.
Solution: The number of digits to the right of the
3. Subtract the original equation from the new
decimal point is 2. Therefore, we will move the decimal
equation (in step 2).
point 2 places to the right and place 77 over 100. So
4. Solve for n and reduce to lowest terms.
Example: Convert 0.2 to a fraction.
Example: Convert -0.045 to a fraction and reduce
Solution: First, let n equal the repeating decimal, or
to lowest terms.
n = 0.222...
Solution:
Second, multiply both sides of the equation by 10 since
there is only one digit in the repeating pattern. Hence,
10n = 2.222...
Third, subtract the original equation from the new
equation. That is,
When converting mixed decimals to fractions, you
will usually find it is easier to keep the integer portion
as an integer and change the decimal fraction to a
common fraction.
Fourth, solve for n.
Example: Convert 12.625 to a fraction and reduce
to lowest terms.
9n = 2
Solution:
14-5



