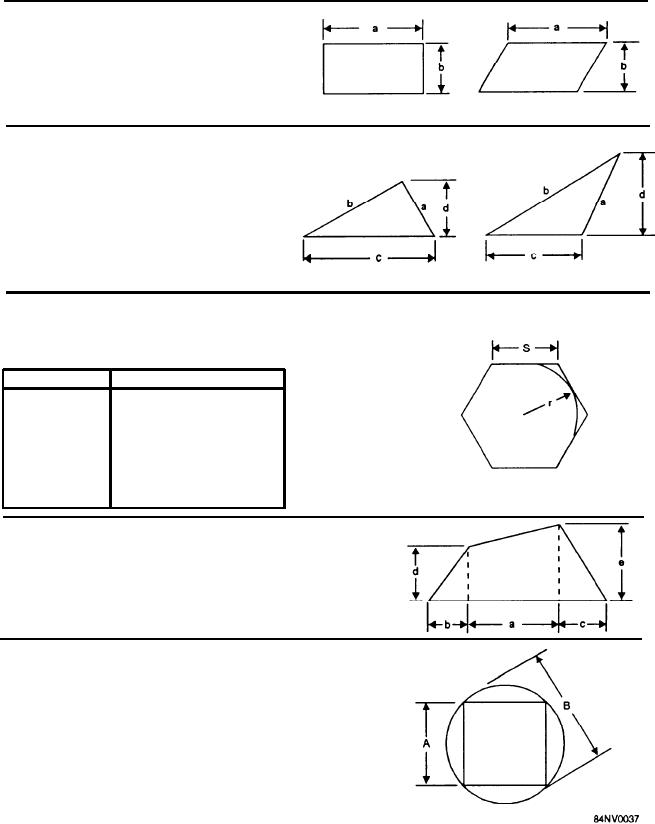
Rectangle and Parallelogram
Area = ab
Triangle
Area = cd.
Example: d = 5"
c = 6"
Then, 5" 6" = 15 sq. in.
Regular Polygons
n = Number of sides, s = Length of one side, r = Inside radius
Area = nsr
Number of Sides
Area
2
r2
5
1.72047
s = 3.63273
s2 = 3.46408
r2
6
2.59809
s2 = 3.37099
r2
7
3.63395
s2 = 3.31368
r2
8
4.82847
s2 = 3.27574
r2
9
6.18181
s2 = 3.24922
r2
10
7.69416
s2 = 3.22987
r2
11
9.36570
s2 = 3.21539
r2
12
11.19616
Trapezium
Area = [ a (e + d) + bd + ce]
Example: a = 10", b = 3", c = 5", d = 6", e = 8"
Area = [ 10 (8 + 6) + (3 6) + (5 8)] = 99 sq. in.
Square
The diagonal of a square = A X 1.414
The side of a square inscribed
in a given circle is B X 0.707.
Figure 14-37.--Areas and volumes for calculating weights of castings.
A = 1/2[a(e + d) + bd + ce]
be enclosed in brackets. The reverse is not true. The
values enclosed by parentheses must be calculated
A = 1/2[10(8 + 6) + 3 x 6 + 5 8]
before the values within brackets. As an example, find
A = 1/2[10(14) + 18 + 40]
the area of a trapezium using the formula and values
shown in figure 14-37.
A = 1/2[140+18 + 40]
14-20



