Figure 10-8.-Equal pressure applied at each end of a tube
containing a liquid.
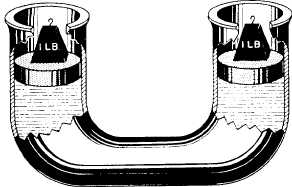
Figure 10-9.-A mechanical advantage of 10.
1-pound weight on each piston, however, each one will
remain in its original position, as shown in figure 10-8.
Thus, you see that a pressure of 1 pound per square
inch applied downward on the right-hand piston exerts
a pressure of 1 pound per square inch upward against
the left-hand one. Not only does the force transmit
through the liquid around the curve, it transmits equally
on each unit area of the container. It makes no difference
how long the connecting tube is or how many turns it
makes. It is important that the entire system be full of
liquid. Hydraulic systems will fail to operate properly if
air is present in the lines or cylinders.
Now look at figure 10-9. The piston on the right has
an area of 1 square inch, but the piston on the left has an
area of 10 square inches. If you push down on the
smaller piston with a force of 1 pound, the liquid will
transmit this pressure to every square inch of surface in
the system. Since the left-hand piston has an area of 10
square inches, each square inch has a force of 1 pound
transmitted to it. The total effect is a push on the larger
piston with a total force of 10 pounds. Set a 10-pound
weight on the larger piston and it will support the
1-pound force of the smaller piston. You then have a
1-pound push resulting in a 10-pound force. That’s a
mechanical advantage of 10. This mechanical advantage
is why hydraulic machines are important.
Here’s a formula that will help you to figure the
forces that act in a hydraulic machine:
In that,
FI = force, in pounds, applied to the small piston;
Fz = force, in pounds, applied to the large piston;
Al = area of the small piston, in square inches; and
AZ = area of the large piston, in square inches.
Let’s apply the formula to the hydraulic press shown
in figure 10-10. The large piston has an area of 90 square
inches, and the smaller one has an area of 2 square
inches. The handle exerts a total force of 15 pounds on
the small piston. With what total force could you raise
the large piston?
Write down the formula
Substitute the known values
and
USES OF HYDRAULIC PRESSURE
You know from your experience with levers that
you can’t get something for nothing. Applying this
knowledge to the simple system in figure 10-9, you
know that you can’t get a 10-pound force from a
10-6