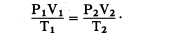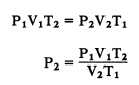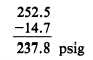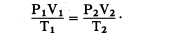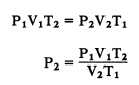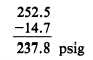GENERAL GAS LAW
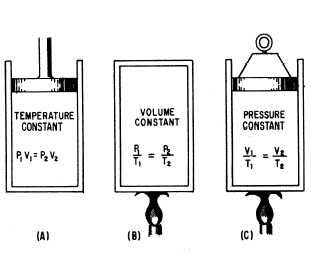
We have learned that Boyle’s law pertains to
situations in which the temperature remains
constant (fig. 11-4), and that Charles’s law
pertains to situations in which pressure remains
constant (fig. 11-4). It is usually not possible to
control pressure or temperature in tanks or bottles
of gas subject to the weather and shipboard
demands. Boyle’s and Charles’s laws are com-
bined to form the general gas law. This law states:
The product of the initial pressure, initial volume,
and new temperature (absolute scale) of an
enclosed gas is equal to the product of the new
pressure, new volume, and initial temperature. It
is a mathematical statement which allows many
gas problems to be solved by using the principles
of Boyle’s law and/or Charles’s law. The equation
is expressed as
or
(P and T represent absolute pressure and absolute
temperature, respectively.)
You can see by examining figure 11-4 that the
three equations are special cases of the general
equation. Thus, if the temperature remains
constant, T1 equals T2 and both can be eliminated
from the general formula, which then reduces to
the form shown in part A. When the volume
remains constant, V1 equals V2, thereby reducing
Figure 11-4.—The general gas law.
the general equation to the form given in part B.
Similarly, P1 is equated to P2 for constant
pressure, and the equation then takes the form
given in part C.
The general gas law applies with exactness only
to “ideal” gases in which the molecules are
assumed to be perfectly elastic. However, it
describes the behavior of actual gases with
sufficient accuracy for most practical purposes.
Two examples of the general equation follow:
1. Two cubic feet of a gas at 75 psig and 80°F
are compressed to a volume of 1 cubic foot and
then heated to a temperature of 300°F. What is
the new gauge pressure?
Using equation 11-9, P1V1T2 = P2V2T1, where
V1 is 2 ft3, P1 is 75 psig, T1 is 80°F, V2 is 1 ft3
and T2 is 300°F:
Solution:
Substituting:
Converting absolute pressure to gauge pressure:
2. Four cubic feet of a gas at 75 psig and 80°F
are compressed to 237.8 psig and heated to a
temperature of 300°F. What is the volume of the
gas resulting from these changes? Using equation
11-9, P1V1T2 = P2V2T1, where V1 is 4 ft3, P2 is
11-6