COPYING OR TRANSFERRING AN
ANGLE
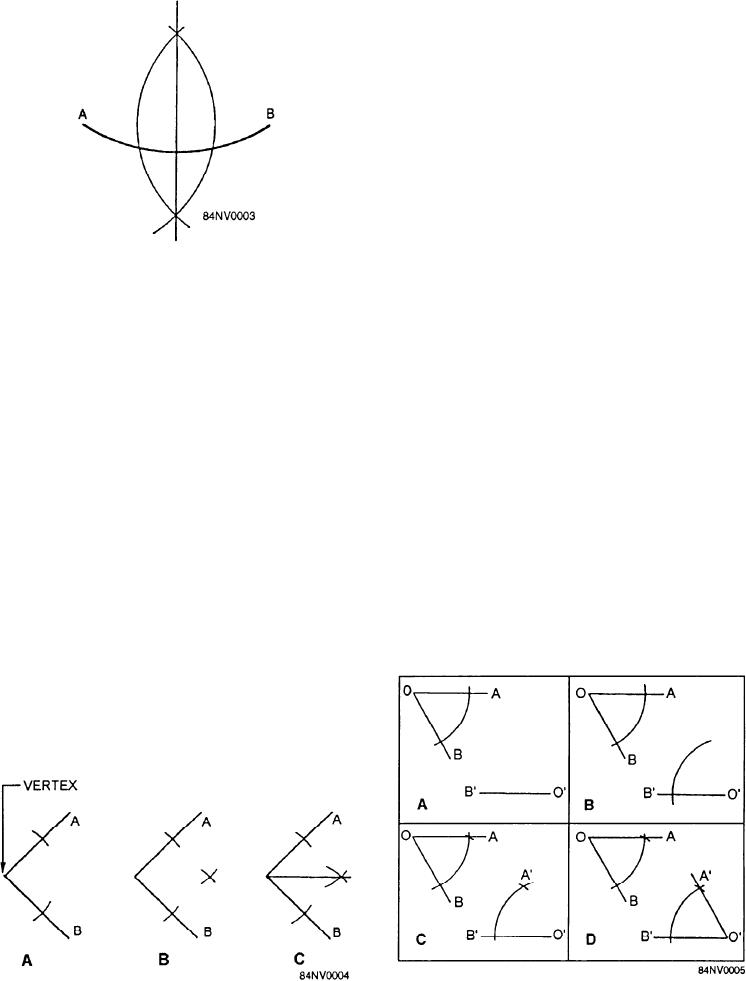
A simple geometrical method can be used to copy
or transfer an angle. Figure 14-5 shows you how to do
this. To use this method, use the following steps to copy
angle AOB onto base line BO:
1. Insert one point of the dividers at point 0 (view
A). Adjust the other leg to intersect line AO at
a distance that is convenient to work with.
2. Draw an arc that intersects both legs of the angle
(view A).
3. Look at view B. Without changing the
Figure 14-3.--Bisecting an arc.
adjustment on the dividers, place the point on
point O and draw an arc intersecting the base
BISECTING AN ARC
line.
To bisect an arc, you should follow the same steps
4. Look at view C. Use the dividers to measure
as those given for bisecting a line. Use the ends of the
between the legs of the angle where the arc cuts
arc (points A and B in fig. 14-3) as centers for the arcs
the legs. Transfer this measurement to line OB
that intersect.
by placing one point of the dividers at the
intersection of line OB and the transferred arc.
BISECTING AN ANGLE
Draw a short arc that intersects the transferred
are (view C).
Look at figure 14-4 as you read about bisecting an
5. Connect the intersection point of the two arcs to
angle. Use the following steps to bisect an angle:
point O to draw leg AO and form AOB (view
1. Use the vertex of the angle as the center for one
D).
point of the dividers. Draw arcs cutting the legs
of the angle (view A).
DIVIDING A LINE INTO FIVE EQUAL
2. Use the intersections of the arcs and the legs as
PARTS
centers to draw arcs that intersect each other
inside the angle (view B).
You may wonder, why not just measure and divide
into the required number of parts? This is not a very
3. Connect the intersection point of these last two
arcs with the vertex of the angle to bisect the
angle (view C).
Figure 14-5.--Copying an angle.
Figure 14-4.--Bisecting an angle.
14-8