straight but the sides are tapered. The center line of the
teeth will intersect at a given point.
Bevel gears are usually manufactured on gear-
cutting machines. However, you will occasionally have
to make one on a universal milling machine.
This section of the chapter deals with the angle
nomenclature of a bevel gear as well as the development
of the triangles needed to manufacture one.
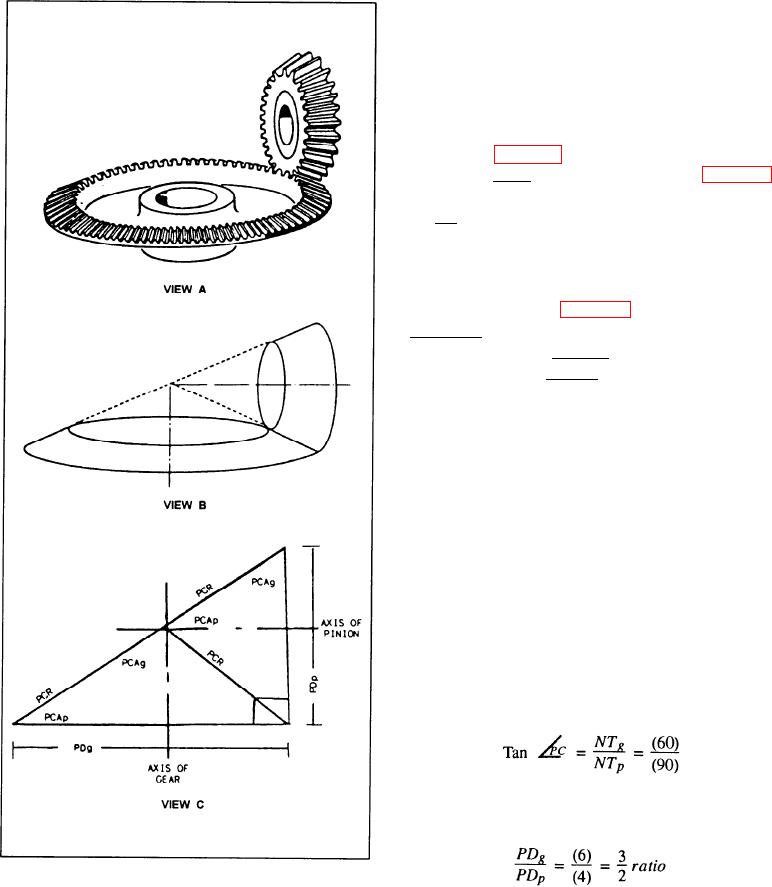
When two bevel gears whose shaft angles equal 90
are in mesh (fig. 14-14, view A) they form a triangle. It
is called the mating gear triangle. The cones (fig. 14-14,
view B) that form the basis of the bevel gears are called
the pitch cones. These cones are not visible at all on the
finished gear, but they are important elements in bevel
gear design.
The angle that is formed at the lower left-hand
corner of the triangle (fig. 14-14, view C) is called the
pitch cone angle of the pinion. The altitude of the
triangle is called the pitch diameter of the pinion, and
its base is called the pitch diameter of the gear.
The hypotenuse of the triangle is twice the pitch
cone radius.
The pitch diameter (gear and pinion), the number
of teeth (gear and pinion), and the actual ratio between
the gear and the pinion are all in ratio. Therefore, we
can use any of these three sets to find the pitch cone
angle (PCA).
Example: A 10 diametral pitch (DP) gear with 60
teeth has a pitch diameter (PD) of 6 and a 10 DP pinion
with 40 teeth has a PD of 4. Therefore, the ratio of the
gear and the pinion is 3:2.
We can determine the PCA by simply substituting
the known values into the formula:
or
Figure 14-14.--Development of the mating gear triangle.
NOTE: The pitch cone angle of the pinion (PCA p)
is the compliment of the pitch cone angle of the gear
(PCAg).
14-15



