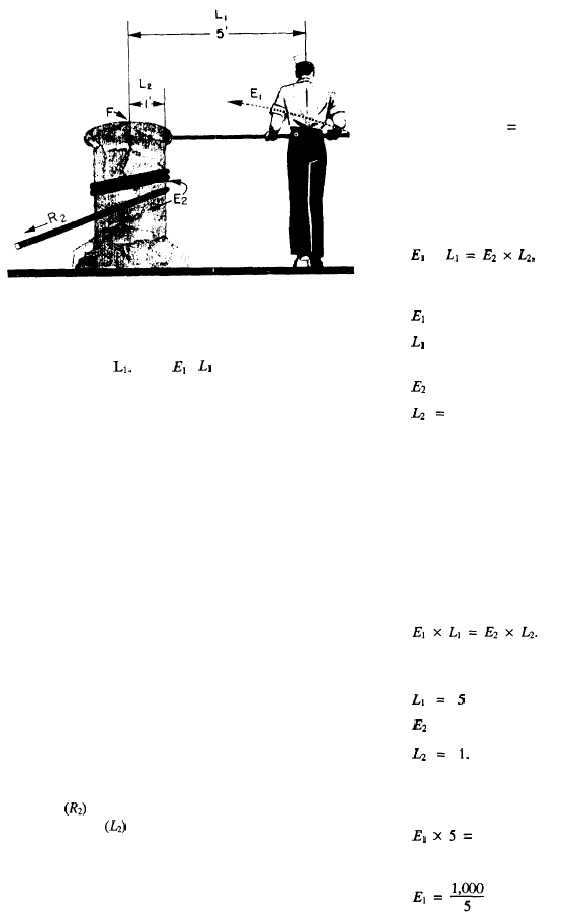
Figure 3-4.-Using the capstan.
of the axle is L1. Then, EI x LI is the moment of force.
You’ll notice that this term includes both the amount of
the effort and the distance from the point of application
of effort to the center of the axle. Ordinarily, you
measure the distance in feet and the applied force in
pounds.
Therefore, you measure moments of force in foot-
pounds (ft-lb). A moment of force is frequently called a
moment.
By using a longer capstan bar, the sailor in figure
3-4 can increase the effectiveness of his push without
making a bigger effort. If he applied his effort closer to
the head of the capstan and used the same force, the
moment of force would be less.
BALANCING MOMENTS
You know that the sailor in figure 3-4 would land
flat on his face if the anchor hawser snapped. As long as
nothing breaks, he must continue to push on the capstan
bar. He is working against a clockwise moment of force
that is equal in magnitude, but opposite in direction, to
his counterclockwise moment of force. The resisting
moment, like the effort moment, depends on two factors.
In the case of resisting moment, these factors are the
force (Rz) with which the anchor pulls on the hawser and
the distance (L-J from the center of the capstan to its rim.
The existence of this resisting force would be clear if the
sailor let go of the capstan bar. The weight of the anchor
pulling on the capstan would cause the whole works to
spin rapidly in a clockwise direction—and good-bye
anchor! The principle involved here is that whenever
the counterclockwise and the clockwise moments of
force are in balance, the machine either moves at a
steady speed or remains at rest.
This idea of the balance of moments of force can be
summed up by the expression
CLOCKWISE
COUNTERCLOCKWISE
MOMENTS
MOMENTS
Since a moment of force is the product of the
amount of the force times the distance the force acts
from the center of rotation, this expression of equality
may be written
El x ~] =Ezx L2,
in that
EI =
force of effort,
L1 =
distance from fulcrum or axle to point
where you apply force,
Ez =
force of resistance, and
h=
distance from fulcrum or center axle to
the point where you apply resistance.
EXAMPLE 1
Put this formula to work on a capstan problem. You
grip a single capstan bar 5 feet from the center of a
capstan head with a radius of 1 foot. You have to lift a
1/2-ton anchor. How big of a push does the sailor have
to exert?
First, write down the formula
Here
LI=5
Ep =
1,000 pounds, and
L2=l.
Substitute these values in the formula, and it
becomes:
E1 X5=
1,000 x 1
and
= 200 pounds
3-3