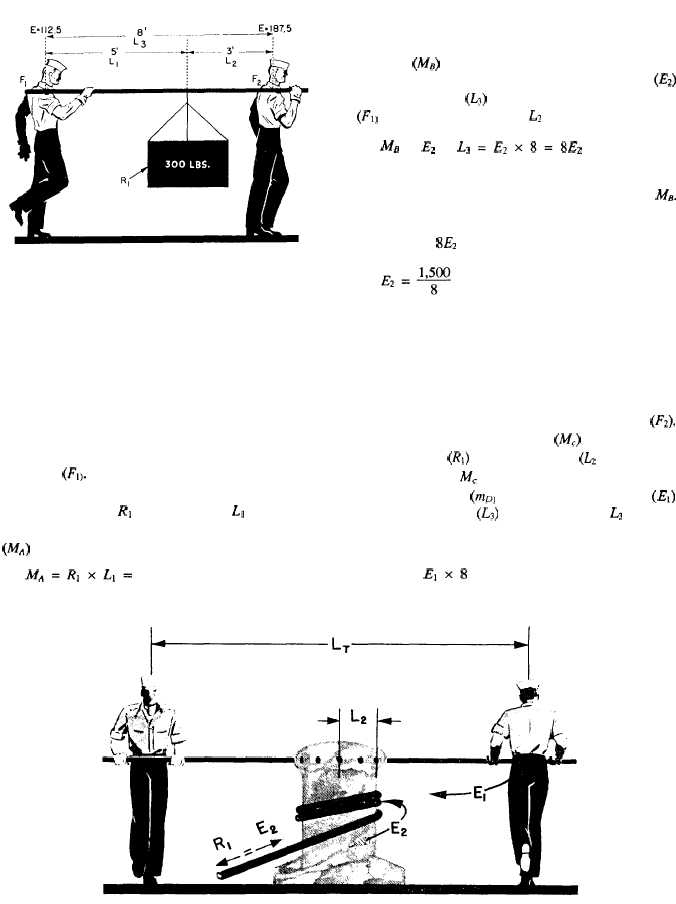
Figure 3-5.-A practical application.
Example 2
Consider now the sad case of Slim and Sam, as
illustrated in figure 3-5. Slim has suggested that they
carry the 300-pound crate slung on a handy 10-foot pole.
He was smart enough to slide the load up 3 feet from
Sam’s shoulder.
Here’s how they made out. Use Slim’s shoulder as
a fulcrum (Fl). Look at the clockwise movement caused
by the 300-pound load. That load is 5 feet away from
Slim’s shoulder. If RI is the load, and Ll the distance
from Slim’s shoulder to the load, the clockwise moment
(MA) is
A4~=R1xLl= 300 x 5 = 1,500 ft-lb.
With Slim’s shoulder still acting as the fulcrum, the
resistance of Sam’s effort causes a counterclockwise
moment (MB) acting against the load moment. This
counterclockwise moment is equal to Sam’s effort (Ez)
times the distance (LJ) from his shoulder to the fulcrum
(F,, at Slim’s shoulder. Since L~ = 8 ft, the formula is
MB = Ez x L3 =E2X8=8EZ
There is no rotation, so the clockwise moment and
the counterclockwise moment are equal. MA = MB.
Hence
1,500 = 8Ez
= 187.5 pounds.
So poor Sam is carrying 187.5 pounds of the
330-pound load.
What is Slim carrying? The difference between 300
and 187.5 = 112.5 pounds, of course! You can check
your answer by the following procedure.
This time, use Sam’s shoulder as the fulcrum (FI).
The counterclockwise moment (MJ is equal to the
300-pound load (Rl) times the distance (b = 3 feet) from
Sam’s shoulder. Mc 300 x 3 = 900 foot-pounds. The
clockwise moment (m~, is the result of Slim’s lift (EI)
acting at a distance (LJ from the fulcrum. L? = 8 feet.
Again, since counterclockwise moment equals clock-
wise moment, you have
900 = E1X8
Figure 3-6.-A couple.
3-4