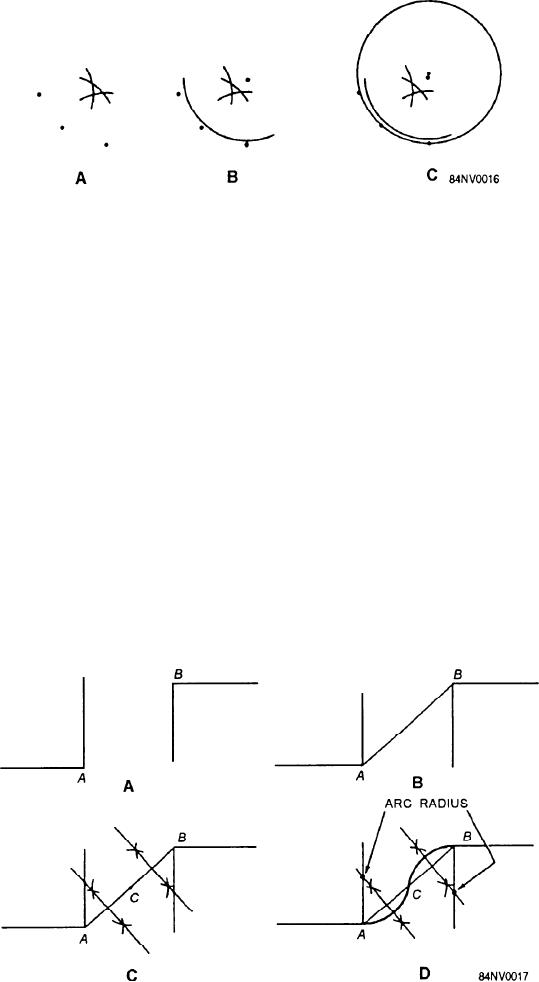
Figure 14-16.--Trial-and-error method of finding the center of a circle that passes through three given points.
Drawing a Reverse or Ogee Curve
The trial-and-error method also can be used in
Tangent to Two Lines
drawing a circle through three given points. In figure
14-16, view A, arcs with an equal radius have been
The following steps tell you how to draw a reverse
drawn from each of the three points. You can see that
or ogee curve. Refer to figure 14-17 as you read this
they fail to have a common point of intersection and are,
section.
therefore, not at the proper center.
1. Erect a perpendicular at point A and drop one at
If the arcs from the two outer points intersect below
point B (view A).
the center point arc (view B), you know that the radius
of the circle is larger. If the two outer points intersect
2. Connect points A and B with a line (view B).
above the center point arc, then the radius of the circle
3. Assume a point (C) on this line through which
is smaller.
the curve will pass. This point may be the
From this trial you can judge where the center will
midpoint of the line if equal arcs are desired.
probably fall. Select a point (O) to use as the center in
4. Bisect AC and CB, as shown in view C. The
drawing your first trial arc. If this trial arc fails to pass
i n t e r s e c t i o n of these lines with the
through the three points perfectly (view B), move the
perpendiculars from points A and B are the
center, as shown in view C.
centers of the required arcs. Complete the
This time you can judge the position of the center
curve, as shown in view D.
so accurately that the circle may be drawn through the
points (view C).
Figure 14-17.--Reverse or ogee curve.
14-12

