The mathematical relationship for kinetic
energy is stated in the rule: “Kinetic energy in
foot-pounds is equal to the force in pounds which
created it, multiplied by the distance through
which it was applied, or to the weight of the
moving object in pounds, multiplied by the square
of its velocity in feet per second, and divided by
64.s”
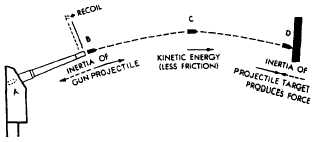
The relationship between inertia forces,
velocity, and kinetic energy can be illustrated by
analyzing what happens when a gun fires a
projectile against the armor of an enemy ship. (See
fig. 2-17.) The explosive force of the powder in
the breach pushes the projectile out of the gun,
giving it a high velocity. Because of its inertia,
the projectile offers opposition to this sudden
velocity and a reaction is set up that pushes the
gun backward (kick or recoil). The force of the
explosion acts on the projectile throughout its
movement in the gun. This is force acting through
a distance producing work. This work appears as
kinetic energy in the speeding projectile. The
resistance of the air produces friction, which uses
some of the energy and slows down the projectile.
Eventually, however, the projectile hits its target
and, because of the inertia, tries to continue
moving. The target, being relatively stationary,
tends to remain stationary because of its inertia.
The result is that a tremendous force is set up that
either leads to the penetration of the armor or
the shattering of the projectile. The projectile
is simply a means of transferring energy, in
this instance for destructive purpose, from the
gun to the enemy ship. This energy is transmitted
in the form of energy of motion or kinetic
energy.
A similar action takes place in a fluid power
system in which the fluid takes the place of the
projectile. For example, the pump in a hydraulic
Figure 2-17.—Relationship of inertia, velocity, and kinetic
energy.
system imparts energy to the fluid, which
overcomes the inertia of the fluid at rest and
causes it to flow through the lines. The fluid flows
against some type of actuator that is at rest. The
fluid tends to continue flowing, overcomes the
inertia of the actuator, and moves the actuator
to do work. Friction uses up a portion of the
energy as the fluid flows through the lines and
components.
RELATIONSHIP OF FORCE,
PRESSURE, AND HEAD
In dealing with fluids, forces are usually
considered in relation to the areas over which they
are applied. As previously discussed, a force
acting over a unit area is a pressure, and pressure
can alternately be stated in pounds per square inch
or in terms of head, which is the vertical height
of the column of fluid whose weight would
produce that pressure.
In most of the applications of fluid power in
the Navy, applied forces greatly outweigh all other
forces, and the fluid is entirely confined. Under
these circumstances it is customary to think of the
forces involved in terms of pressures. Since the
term head is encountered frequently in the study
of fluid power, it is necessary to understand what
it means and how it is related to pressure and
force.
All five of the factors that control the actions
of fluids can, of course, be expressed either as
force, or in terms of equivalent pressures or head.
In each situation, the different factors are referred
to in the same terms, since they can be added and
subtracted to study their relationship to each
other.
At this point you need to review some terms
in general use. Gravity head, when it is important
enough to be considered, is sometimes referred
to as head. The effect of atmospheric pressure is
referred to as atmospheric pressure. (Atmospheric
pressure is frequently and improperly referred to
as suction.) Inertia effect, because it is always
directly related to velocity, is usually called
velocity head; and friction, because it represents
a loss of pressure or head, is usually referred to
as friction head.
STATIC AND DYNAMIC FACTORS
Gravity, applied forces, and atmospheric
pressure are static factors that apply equally to
2-13