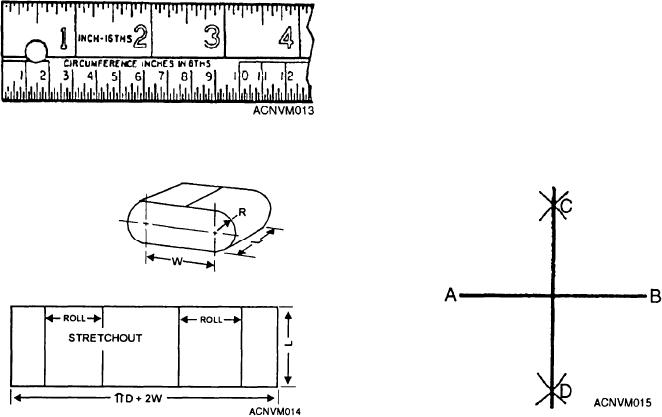
If you compute the circumference, multiply the
shape, which we will say is 12 inches. The second is the
diameter by pi (š), or 3.1416. This formula is read as
circumference, which is computed as follows. Use the
formula C = šD + 2W. D is the diameter of the circle
C = šD. If the measurement is not critical, you can
that you would have if both curved ends of the shape
round off pi to 3.14 or 3 l/7. Either way, the formula
were put together. W is shown in figure 12-14. We will
will give you one dimension of your stretchout. The
assume that D = 5 inches, and W = 6 inches.
height or length is your other dimension.
C = šD+2W
Another method is by the use of the circumference
rule. The upper edge of the circumference rule is
C = 3.14 5+2 6
graduated in inches in the same manner as a regular
layout scale, but the lower edge is graduated, as shown
C = 15.7 + 12
in figure 12-13.
C = 27.7
The lower edge gives you the approximate
We find that the circumference is 27.7 inches.
circumference of any circle within the range of the rule.
Therefore, our stretchout measures 27.7 inches by 12
You will notice in figure 12-13 that the reading on the
inches.
lower edge directly below the 3-inch mark is a little over
9 3/8 inches. This reading would be the circumference
of a circle with a diameter of 3 inches and would be the
USING GEOMETRY FOR LAYOUTS
length of a stretchout for a cylinder of that diameter. The
dimensions for the stretchout of a cylindrical object,
Following are the procedures in using geometry for
then, are the height or length of the cylinder and the
making various types of layouts.
circumference. Do not forget that you will have to allow
for the scams.
CONSTRUCT A 90-DEGREE OR RIGHT
ANGLE. This is no problem at all if you have a true
A VARIATION OF THE CYLINDRICAL JOB is
steel square. We will describe three methods that you
a flat-sided structure with rounded ends (fig. 12-14).
may use to erect a perpendicular to produce a right angle
To figure the stretchout for this shape, you will need
when you do not have a usable true steel square.
two dimensions. The first is simply the length of the
1. For the first method, break out your dividers, a
scriber, and a straightedge. Draw a base line like the one
labeled AB in figure 12-15. Set the dividers for a
distance greater than one-half AB, then, with A as a
center, scribe arcs like those at C and D. Then, without
changing the setting of the dividers, use B as a center,
and scribe another set of arcs at C and D. Draw a line
through the points where the arcs intersect and you will
have perpendiculars to line AB, forming four 90-degree
Figure 12-13.--Circumfcrcncc rule.
or right angles. Not only have you constructed a
Figure 12-15.--Constructing a 90-degree angle by bisecting a
Figure 12-14.--Variation of a cylinder.
line.
12-5

